6 minutes
Irradiance & Radiance
This is an updated repost of my deactivated old blog or from notes of past my studies. The date follows the original time of writing
Introduction
Rendering is an evolving science, every day new papers are published, new posts show up on our twitter feed and we learn new techs, tricks and mathematical proofs. With new technologies comes new topics to be studied and applied, but the foundations stand still as the build blocks, constant over time (most of times at least!).
Shading, the act of computing the final intensity - actually is the radiance, but you can think of it as intensity for now! - of a pixel, is one of the most important topics inside rendering, new techniques are always showing up as the entire field converges to a physically based model. This convergence is great and also the next logical step as the most realistic model of how light interacts with matter is the real world.
For a complete and correct representation of light-matter interaction we need a way to rigorous represent light, this field already exist and is called Radiometry (the physics of how we represent and measure light.). Therefore we can work with things as intensity of beans and accumulation (reads average or integration!) of light in a certain point in space. This quantities are the basic building blocks for the physically based treatment of light in rendering and the focus of this post.
Irradiance
Irradiance is the measure of incoming light flux per meter square, in resume that is all, but let's analyze what this statement means. A point I want to make is that this quantity doesn't depend on direction, it is like a mean of the total light flux reaching the surface on each point.
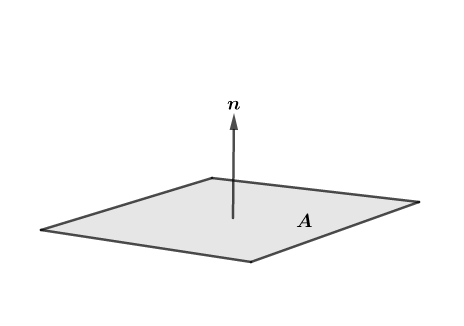
Working with figure 1 we can make this ideia more visual. We can look at Irradiance as the average of the light flux coming from various directions relative to the normal, thus working as if the entire plane had a constant light flux passing through its surface. Therefore we define Irradiance as:
\[E(n) = \frac{1}{A}\sum_{i=0}^{N}\Phi_i \tag{I} \]
This definition give us a more intuitive understand of what Irradiance is, although we can also define Irradiance in term of differentials:
\[E(n) = \frac{d\Phi}{dA} \tag{II} \]
Definition \(II\) works on a point (a differential area) while \(I\) works on areas, thus if you wan to express the concept of Irradiance on points with differential flux you must use \(II\), as \(I\) gives constant Irradiance for all points belonging to the surface area.
Radiance
We saw the notion of flux passing through area as a measure of surface's brightness, now we turn our focus to the light beans itself, let's see how we can measure this same notion, but now for the light beans coming in a certain direction.
Before we define radiance we need to define what is a solid angle. In simple terms a solid angle is an analogous of a angle in 2D, but now in 3-dimensions.
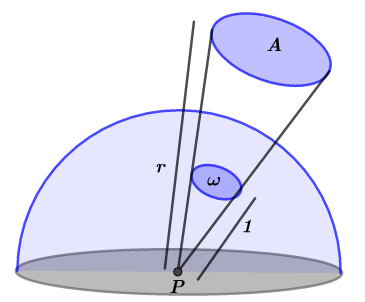
A more intuitive way to think about this is as follows (see Figure 2): Imagine you are on point \(P\) looking at the direction of cone \(\omega\) , even though \(A\) is greater than your relative area of vision \(\omega\) you still can see it because it is farther away, thus \(\omega\) acts like the projection of \(A\) on the hemisphere, therefore \(P\) sees \(A\) and \(\omega\) as the same. Think about this for a while, you will see why this is true.
Well, hopefully we now have a intuition about what a solid angle is, but we also need need a formula to compute it.
Assuming that \(A\) is part of a greater sphere of radius \(r\) and assuming that \(\omega\) belong to the surface's area of the unit sphere we can get the following relation:
\[ \frac{4\pi}{4\pi r^{2}} = \frac{\omega}{A} \implies \omega = \frac{A}{r^{2}} \tag{III} \]
This is the inverse square law. Imagine that \(P\) now is a point light source and \(\omega\) is the first area that the flux being emitted by \(P\) pass through, we can't create light, we are excluding emmiters. So the same flux that passed on \(\omega\) must pass on \(A\) too, but \(A\) is \(r^{2}\) greater than \(\omega\), therefore \(A\) must be less bright than \(\omega\) and this factor is exactly \(\frac{1}{r^2}\).
Now we define radiance:
\[ L(\Psi) = \frac{d\Phi}{dA_{\bot}d\omega_{i}} \tag{IV} \]
Actualy, the more formal definition of Radiance uses partial derivatives and accounts for time variations, polarization and wavelength dependence. We ignore all those factors here. Glassner - Volume I: Chapter 13 gives a great explanation of why such simplification still valid for our objectives.
Is more helpful to write \(dA_{\bot}\) in function of \(dA\), thus we have:
\[ L(\Psi) = \frac{d\Phi}{dA\cos{\theta}d\omega} \tag{V} \]
The proof of the relation \(dA_{\bot} = dA\cos{\theta}\) is left as a exercice to the reader! (Hint: \(dA_{\bot}\) is parallel to beam of light and \(dA\) to the surface normal)
Now let's analyze \(V\):
As we know radiance is the quantity used to measure light coming in certain direction (in our case \(\Psi_i\)) with a certain flux associated to this direction. Therefore we must account both for direction and intensity. The solid angle controls the fading of the light with distance and also the projection notion as explained before, thus is the one which accounts for the fading of the flux, therefore influencing on the intensity factor. The directional component is controlled by \(cos\theta_i\), the one which controls the projection of the parallel surface on the true surface area, thus controlling how much the of the incoming flux the true surface receives.
Now that both Radiance and Irradiance are explained and defined we relate the two:
\(L(\Psi_i) = \frac{d\Phi}{dAcos\theta_i d\omega_i} = \frac{E(n)}{cos\theta_i d\omega_i} \implies E(n) = L(\Psi_i)cos\theta_id\omega_i \tag{VI} \) The equation above give us the differential Irradiance \(II\), therefore if we want to work with the finete Irradiance \(I\) we must integrate this differential Irradiance, thus accounting for all directions above our point \(P\):
\[E(n) = \int_{\Omega(n)}L(\Psi_i)cos\theta_id\omega_i \tag{VII}\]
A point must be made about \(VII\):
Even though \(I\) and \(VII\) returns finite values for points them differ in nature, \(I\) assumes a constant Irradiance across the entire surface, but \(VI\) does not as you can integrate the Irradiance of entire surface in function of the normals of each point, thus getting different values for each. In a plane \(I\) and \(VI\) are exactly the same though.
That is it, until next time!
And Live long and Prosper!
1092 Words
2017-11-12 21:00 -0300