Introduction

Back in 2017 I wrote a post on the basics of Radiance and Irradiance. Although nothing is wrong with the concepts explained in the text, there are some flaws in how core fundamentals are presented. This post is a more detailed introduction to the topic with intention of better explain those fundamental quantities. Beware! this is a BRAIN DUMP!

So, What is Radiance?

Normally, Radiance is thought of as energy per ray of light. This makes sense and is coherent with the units of radiance:

\[ L(\vec{r},\hat{v}) = \frac{d\phi}{dAcos\theta d\omega} \space \begin{bmatrix} \frac{W}{m^2sr} \end{bmatrix} \]

The omission starts to bubble up when is time to explain the flux \( d\phi \). Most of times, there is no explanation on what is this flux, how it is defined or even what it really means. The texts just say is some kind of radiant flow in space and that's it! Actually, during my reads of scattered materials in the internet I found 2 texts (1st, 2nd), inside the rendering community, that actually explained this flux.

I'm going to define the Radiance from basic principles with the help of probability theory, but bare in mind that this is not a academic textbook nor a research paper. Again, this is a brain dump!

First, we need to understand what we are measuring. To help with the thought process the image bellow will be used:

Figure 1
Figure 1 - Photons inside a little "box"

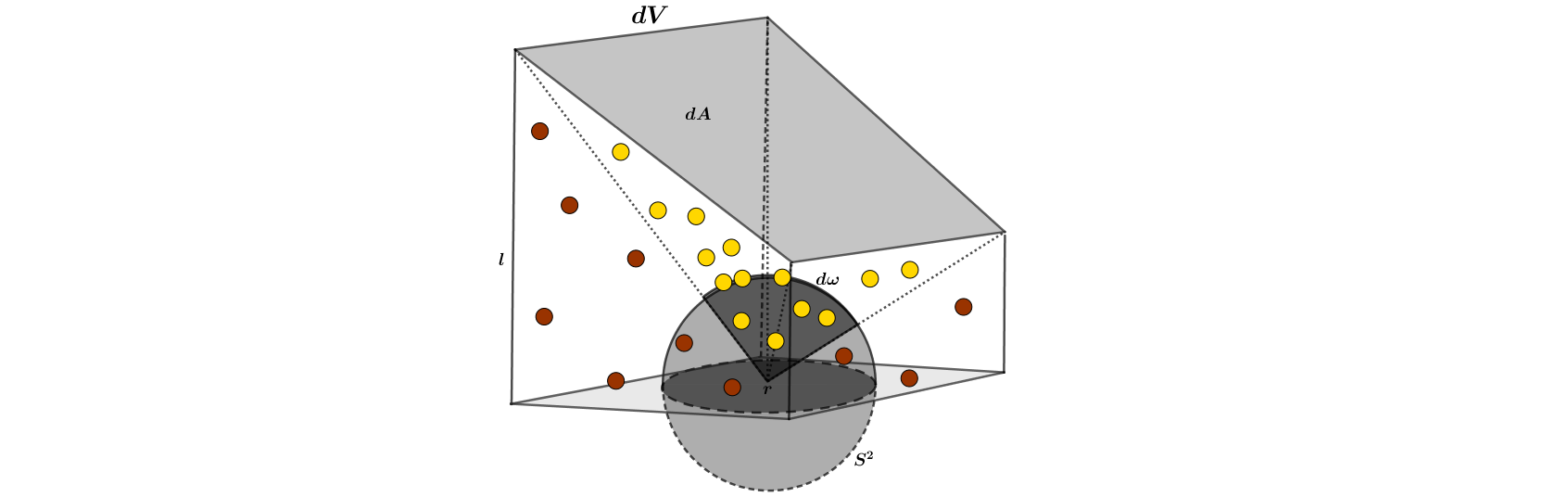
Well, we know that there is a little guy called Photon that is the smallest possible discrete piece of light. Thus, if we know how much of those guys we have and how much energy each of them posses we can calculate the radiant energy inside a ray, right? Let's see.

Assume we have a little volume \(dV\) and inside there is a discrete amount of photons given by the function \(\epsilon (x)\) (We could follow some rigorous definitions for this function and prove proprieties, instead we won't! See here for good rigorous proofs). Thus, the energy \( E \) per little volume in space is how much photons we have times the energy of each one. Mathematically speaking we have:

\[ E = \frac{\epsilon (x)E_{photon}}{dV} \]

The energy of the photon is known and is equal to \( hv \). In which \(h\) is the Planck's constant and \(v\) is its frequency, thus:

\[ E = \frac{\epsilon (x)hv}{dV} \]

Now we have energy per volume, but wait! We want energy per ray. Therefore, is necessary the addition of a angular component. See the figure above: The yellow photons are inside the solid angle \( d \omega \) and thus are part of the differential "ray" in the specified direction. While the other photons belongs to \(dV\) they do not contribute in the direction of \( \omega \). Thus, correcting for angular dependency we have:

\[ E = \frac{\epsilon (x)hv}{dV d \omega} \]

Great, now we have photons inside a ray! But, why are they not moving? They are! Actually, what we did was take a snapshot of one specific time \(dt\). In general we have:

\[ E' = \frac{\epsilon (x)hv(cdt)}{dV d \omega} \]

Now we have \( E'\), but if you're paying attention you probrably already known that \( E'\) is actually the Radiance at point \(r\) and direction \(\omega\). Don't believe? Let's rearrange things. First, the velocity of a photon is \(c\) and velocity is defined as space per time, thus \( ds = cdt \). But, in our case \(ds = l\), the height of the solid angle, and \(dV = ldA\), therefore:

\[ E' = \frac{\epsilon (x)hvl}{ldA_{\perp} d \omega} \]

Canceling the \(l\):

\[ E' = \frac{\epsilon (x)hv}{dA_{\perp} d \omega} \space \begin{bmatrix} \frac{W}{m^2sr} \end{bmatrix} \]

To conclude, \( \epsilon (x)hv \) is how much energy pass in the area \(dA\) per time \(dt\) with velocity \(c\), mathematically \( d\phi = \epsilon (x)hv \). Therefore:

\[ E' = L\]

That is it, until next time! And Live long and Prosper!