Hello Folks! How your molecules doing?

Introduction

Back in the day in a forgotten time, I was totally immerse in the J.R.R Tolkien's Eä. I would always try to imagine the landscapes and scenes described in his books - you know! Tolkien gave descriptions to everything. Really, everything. From all the written details he gave, something always caught my attention: the duality present between light and dark.

A great implementation of this concept is Battle for Wesnoth day/night cycles - lawful vs chaotic units. Besides being a great game there also some really great storytelling there. Also it is Open Source!

Being a nerd, choosing a fantasy/sci-fi (... and metal) background was a obvious course of action when developing the first demo of my beloved engine. I would need to reference something I like (I always do this) and the idea of an island was already in my mind, maybe because of Crash Bandicoot 1 map, IDK!

During the first days of development I was on a Megadeth marathon and stumbled uppon the song Devil's Island from the Peace Sells... but Who's Buying? album. The moment I heard the song I thougth: Snap! Got my theme. After some research, I also discovered that Star Trek TOS made some references to the Devil's Island. From this point I had no doubt for my demo theme: An Island. And this was how my technical trip through the engine room started! Ask Garrus or Geordi, If you don't belive me!

So, in today's wizardry trek we talk about shadows and how I decided to use baked horizon maps. Whether it was a bad decision or not I'll only know for sure when I finished the demo. But for now let's take a trip through the land where the shadows lie.

Without further ado let's go!

Part I - Selecting a Shadowing Method

As you probably know the standard method for rendering real-time shadows is Shadow Mapping [1]. And this was my first weapon of choice, but during my research for an atmospheric rendering solution I found a 2001 GDC paper [2] which used a technique called Horizon Mapping [3] as a pre-pass, I could have sticked to some filtering technique and just use SM instead of trying this algorithm, but the point in question was the possibility of just doing one baking pre-pass for the shadows and used it every-time I ran the demo, even with a dynamic sun-system. This seems like a big win, because I won't have dynamic objects in the scene - just the water, but it's change in height will be much smaller than the heighfield changes in slope, so the probability that the shadow binary function will change it's very small. Although I haven't tested this yet.

Thus, I decided to go with precomputed horizon-map shadows. This is a R&D situation: may work or may not. Either way, is a learning opportunity and what matters is that at the end the demo will have a robust shadowing system, being it horizon maps or shadow-mapping is something that the project itself will tell.

Part II - Finding the Horizon Angles using the DDA Method

The construction process of the horizon map, a.k.a the baking, is very simple: We ray-march in all 8 possible directions in our heightmap - like in a compass rose - and store the minimum horizon angle necessary so the specific point is visible in the selected direction. Nothing new here, just the old DDA method [4]! Look at the figure bellow:

Figure 1
Figure 1 - Wikipedia Compass Rose

So, how we do that? First, assume we are at a point \(P(x,y)\) in our heightmap. Then, the question we want to ask is the following: What is the minimum angle the sun must do with the horizon line so it can see me? We must answer that question for each of the 8 possible directions.

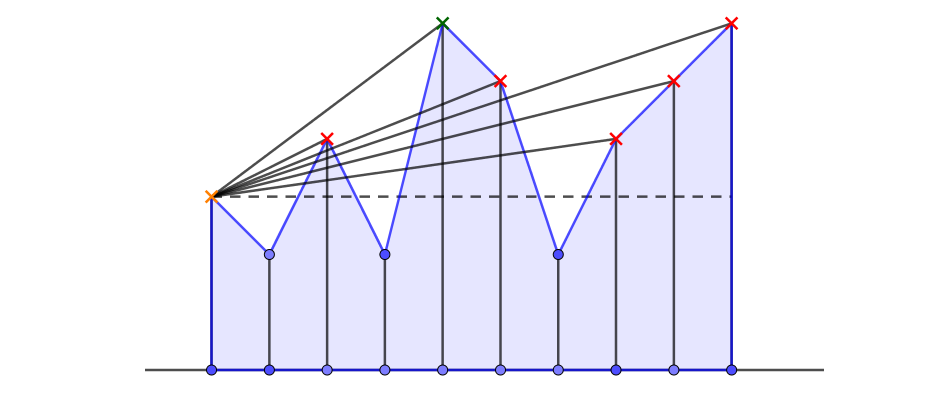
For each direction we do the following: Ray-March from the current starting point \(P(x,y)\) to a new point, let's call it \(P(x,y)_i\). Then, check the angle created by the vector going from \(P(x,y)\) to \(P(x,y)_i\) and the horizon vector, the horizon vector is just the projection of the vector in the x,y plane, If this angle is greater than the current angle \( \phi \) update the horizon angle and iterate again. When the iteration completes we will have the minimum horizon angle for the particular point. This shows the global nature of this algorithms, something expected as shadows are a global phenomenon.

For a visual take on the algorithm look at Figure 2 bellow:

Figure 1
Figure 2 - Horizon Map Angle Computation: This image shows an example of the algorithm at work. The cross-points represents texels who play a role in the process while round ones represents premature texels rejected based on height. This algorithm is global, therefore it must touch all texels that impact the scene in some way. To represent those texels we use the red points while the green point represent the current texel who has the greatest horizon angle. In fact, when the iteration ends the green point will converge to the maxima, all brute-force algorithms sustain that propriety.

Part III - Storing & Sampling the Horizon Map

The next phase is very simple, and is more of a take on API settings than the algorithm per se. As we have 8 angles per texel is clear we can't store a horizon map, without compression, using only one planar texture. There are 2 options to solve this that I am aware of: The first is to use 2 32-bits planar textures, and the second is to use a volume texture. You can argue for both sides depending of your situation. For me 2 linear RGBA8, is simpler and work just fine, see Figure 3.

Figure 1
Figure 3: Horizon Map Stored as 2 Linear RGBA Textures

Now we have only one step to go: Sampling! As it turns out this is another very ease step. We will only need 2 variables to sample the map: The sun radiance's direction a.k.a directional light source and the horizon angle at the moment of sampling.

Finally, project the directional vector on the xy plane and use its contents to select which of the 8 values will be accessed, for example: I used a CCW orientation on the compass rose. Therefore, If the sampled angle is greater than the sun's horizon angle the vertex/fragment is in shadow. That simple!

Well, there is it for today folks! I expect this post helped you in some way. Live Long & Prosper! and until next time.

Results

An example of the algorithm in use is given the figures bellow:

Figure 1
Figure 4: Sun Direct Illumination Only
Figure 1
Figure 5: Sun Direct Illumination + Horizon Maps

References

  • [1] Lance Williams (1978). Casting curved shadows on curved surfaces ACM SIGGRAPH Computer Graphics
  • [2] Naty Hoffman, Kenny Mitchell (2001). Real-Time Photorealistic Terrain Lighting. 2001 Game Developer Conference
  • [3] Max, N. L. (1988). Horizon mapping: shadows for bump-mapped surfaces. The Visual Computer
  • [4] John F. Hughes, James D. Foley, Andries van Dam, Steven K. Feiner Computer Graphics: Principles and Practice in C. Addison–Wesley